Hiện tượng:
mount 192.168.5.21:/San_MobiTv/San_MobiTv_4T/ /San_MobiTv/San_MobiTv_4T
mount.nfs: access denied by server while mounting 192.168.5.21:/San_MobiTv/San_MobiTv_4T/
Cách fix: /etc/init.d/rpcbind restart
Sẽ update thêm lý do sau !
Thứ Năm, 30 tháng 7, 2015
Thứ Tư, 29 tháng 7, 2015
Tips: do something with MySQL without bin_log
SET sql_log_bin = 0;
#some SQL here
truncate table log_transaction;
SET sql_log_bin = 1;
#some SQL here
truncate table log_transaction;
SET sql_log_bin = 1;
Thứ Tư, 22 tháng 7, 2015
How To Use HAProxy to Set Up HTTP Load Balancing on an Ubuntu VPS
About HAProxy
HAProxy(High Availability Proxy) is an open source load balancer which can load balance any TCP service. It is particularly suited for HTTP load balancing as it supports session persistence and layer 7 processing.With the introduction of Shared Private Networking in DigitalOcean HAProxy can be configured as a front-end to load balance two VPS through private network connectivity.
Prelude
We will be using three VPS (droplets) here:Droplet 1 - Load Balancer
Hostname: haproxy
OS: Ubuntu Public IP: 1.1.1.1 Private IP: 10.0.0.100
Droplet 2 - Node 1
Hostname: lamp1
OS: LAMP on Ubuntu Private IP: 10.0.0.1
Droplet 2 - Node 2
Hostname: lamp2
OS: LAMP on Ubuntu Private IP: 10.0.0.2
Installing HAProxy
Use theapt-get command to install HAProxy.apt-get install haproxy
nano /etc/default/haproxy
ENABLED option to 1ENABLED=1
root@haproxy:~# service haproxy
Usage: /etc/init.d/haproxy {start|stop|reload|restart|status}
Configuring HAProxy
We'll move the default configuration file and create our own one.mv /etc/haproxy/haproxy.cfg{,.original}
nano /etc/haproxy/haproxy.cfg
global
log 127.0.0.1 local0 notice
maxconn 2000
user haproxy
group haproxy
log directive mentions a syslog server to which log
messages will be sent. On Ubuntu rsyslog is already installed and
running but it doesn't listen on any IP address. We'll modify the config
files of rsyslog later. The
maxconn directive specifies the number of concurrent connections on the frontend. The default value is 2000 and should be tuned according to your VPS' configuration.The
user and group directives changes the HAProxy process to the specified user/group. These shouldn't be changed.defaults
log global
mode http
option httplog
option dontlognull
retries 3
option redispatch
timeout connect 5000
timeout client 10000
timeout server 10000
timeout directives. The connect option specifies the maximum time to wait for a connection attempt to a VPS to succeed. The
client and server timeouts apply when
the client or server is expected to acknowledge or send data during the
TCP process. HAProxy recommends setting the client and server timeouts to the same value.The
retries directive sets the number of retries to perform on a VPS after a connection failure.The
option redispatch enables session redistribution in case of connection failures. So session stickness is overriden if a VPS goes down.listen appname 0.0.0.0:80
mode http
stats enable
stats uri /haproxy?stats
stats realm Strictly\ Private
stats auth A_Username:YourPassword
stats auth Another_User:passwd
balance roundrobin
option httpclose
option forwardfor
server lamp1 10.0.0.1:80 check
server lamp2 10.0.0.2:80 check
appname which is just a name for identifying an application. The stats directives enable the connection statistics page and protects it with HTTP Basic authentication using the credentials specified by the stats auth directive.This page can viewed with the URL mentioned in
stats uri so in this case, it is http://1.1.1.1/haproxy?stats;a demo of this page can be viewed here.
The
balance directive specifies the load balancing algorithm to use. Options available are Round Robin (roundrobin), Static Round Robin (static-rr), Least Connections (leastconn), Source (source), URI (uri) and URL parameter (url_param).Information about each algorithm can be obtained from the official documentation.
The
server directive declares a backend server, the syntax is:server <name> <address>[:port] [param*]
check and cookie parameters in this article. The check option enables health checks on the VPS otherwise, the VPS isalways considered available.
Once you're done configuring start the HAProxy service:
service haproxy start
Testing Load Balancing and Failover
To test this setup, create a PHP script on all your web servers (backend servers - LAMP1 and LAMP2 here)./var/www/file.php<?php
header('Content-Type: text/plain');
echo "Server IP: ".$_SERVER['SERVER_ADDR'];
echo "\nClient IP: ".$_SERVER['REMOTE_ADDR'];
echo "\nX-Forwarded-for: ".$_SERVER['HTTP_X_FORWARDED_FOR'];
?>
> curl http://1.1.1.1/file.php
Server IP: 10.0.0.1
Client IP: 10.0.0.100
X-Forwarded-for: 117.213.X.X
> curl http://1.1.1.1/file.php
Server IP: 10.0.0.2
Client IP: 10.0.0.100
X-Forwarded-for: 117.213.X.X
> curl http://1.1.1.1/file.php
Server IP: 10.0.0.1
Client IP: 10.0.0.100
X-Forwarded-for: 117.213.X.X
X-Forwarded-For header is your IP.To see how failover works, go to a web server and stop the service:
lamp1@haproxy:~#service apache2 stop
curl again to see how things work.Session Stickiness
If your web application serves dynamic content based on users' login sessions (which application doesn't), visitors will experience odd things due to continuous switching between VPS. Session stickiness ensures that a visitor sticks on to the VPS which served their first request. This is possible by tagging each backend server with a cookie.We'll use the following PHP code to demonstrate how session stickiness works.
/var/www/session.php<?php
header('Content-Type: text/plain');
session_start();
if(!isset($_SESSION['visit']))
{
echo "This is the first time you're visiting this server";
$_SESSION['visit'] = 0;
}
else
echo "Your number of visits: ".$_SESSION['visit'];
$_SESSION['visit']++;
echo "\nServer IP: ".$_SERVER['SERVER_ADDR'];
echo "\nClient IP: ".$_SERVER['REMOTE_ADDR'];
echo "\nX-Forwarded-for: ".$_SERVER['HTTP_X_FORWARDED_FOR']."\n";
print_r($_COOKIE);
?>
Cookie insert method
In this method, all responses from HAProxy to the client will contain aSet-Cookie:
header with the name of a backend server as its cookie value. So going
forward the client (web browser) will include this cookie with all its
requests and HAProxy will forward the request to the right backend
server based on the cookie value.For this method, you will need to add the
cookie directive and modify the server directives under listen cookie SRVNAME insert
server lamp1 10.0.0.1:80 cookie S1 check
server lamp2 10.0.0.2:80 cookie S2 check
Set-Cookie: header with a cookie named SRVNAME having its value as S1 or S2 based on which backend answered the request. Once this is added restart the service:service haproxy restart
curl to check how this works.> curl -i http://1.1.1.1/session.php
HTTP/1.1 200 OK
Date: Tue, 24 Sep 2013 13:11:22 GMT
Server: Apache/2.2.22 (Ubuntu)
X-Powered-By: PHP/5.3.10-1ubuntu3.8
Set-Cookie: PHPSESSID=l9haakejnvnat7jtju64hmuab5; path=/
Expires: Thu, 19 Nov 1981 08:52:00 GMT
Cache-Control: no-store, no-cache, must-revalidate, post-check=0, pre-check=0
Pragma: no-cache
Vary: Accept-Encoding
Content-Length: 143
Connection: close
Content-Type: text/plain
Set-Cookie: SRVNAME=S1; path=/
This is the first time you're visiting this server
Server IP: 10.0.0.1
Client IP: 10.0.0.100
X-Forwarded-for: 117.213.X.X
Array
(
)
Set-Cookie: SRVNAME=S1; path=/. Now, to emulate what a web browser would do for the next request, we add these cookies to the request using the --cookie parameter of curl.> curl -i http://1.1.1.1/session.php --cookie "PHPSESSID=l9haakejnvnat7jtju64hmuab5;SRVNAME=S1;"
HTTP/1.1 200 OK
Date: Tue, 24 Sep 2013 13:11:45 GMT
Server: Apache/2.2.22 (Ubuntu)
X-Powered-By: PHP/5.3.10-1ubuntu3.8
Expires: Thu, 19 Nov 1981 08:52:00 GMT
Cache-Control: no-store, no-cache, must-revalidate, post-check=0, pre-check=0
Pragma: no-cache
Vary: Accept-Encoding
Content-Length: 183
Connection: close
Content-Type: text/plain
Your number of visits: 1
Server IP: 10.0.0.1
Client IP: 10.0.0.100
X-Forwarded-for: 117.213.87.127
Array
(
[PHPSESSID] => l9haakejnvnat7jtju64hmuab5
[SRVNAME] => S1
)
> curl -i http://1.1.1.1/session.php --cookie "PHPSESSID=l9haakejnvnat7jtju64hmuab5;SRVNAME=S1;"
HTTP/1.1 200 OK
Date: Tue, 24 Sep 2013 13:11:45 GMT
Server: Apache/2.2.22 (Ubuntu)
X-Powered-By: PHP/5.3.10-1ubuntu3.8
Expires: Thu, 19 Nov 1981 08:52:00 GMT
Cache-Control: no-store, no-cache, must-revalidate, post-check=0, pre-check=0
Pragma: no-cache
Vary: Accept-Encoding
Content-Length: 183
Connection: close
Content-Type: text/plain
Your number of visits: 2
Server IP: 10.0.0.1
Client IP: 10.0.0.100
X-Forwarded-for: 117.213.87.127
Array
(
[PHPSESSID] => l9haakejnvnat7jtju64hmuab5
[SRVNAME] => S1
)
Cookie Prefix Method
On the other hand, if you want stickiness only for specific cookies or don't want to have a separate cookie for session stickiness, theprefix option is for you.To use this method, use the following
cookie directive:cookie PHPSESSID prefix
PHPSESSID can be replaced with your own cookie name. The server directive remains the same as the previous configuration.Now let's see how this works.
> curl -i http://1.1.1.1/session.php
HTTP/1.1 200 OK
Date: Tue, 24 Sep 2013 13:36:27 GMT
Server: Apache/2.2.22 (Ubuntu)
X-Powered-By: PHP/5.3.10-1ubuntu3.8
Set-Cookie: PHPSESSID=S1~6l2pou1iqea4mnhenhkm787o56; path=/
Expires: Thu, 19 Nov 1981 08:52:00 GMT
Cache-Control: no-store, no-cache, must-revalidate, post-check=0, pre-check=0
Pragma: no-cache
Vary: Accept-Encoding
Content-Length: 143
Content-Type: text/plain
This is the first time you're visiting this server
Server IP: 10.0.0.1
Client IP: 10.0.0.100
X-Forwarded-for: 117.213.X.X
Array
(
)
server cookie S1 is prefixed to the session cookie. Now, let's send two more requests with this cookie.> curl -i http://1.1.1.1/session.php --cookie "PHPSESSID=S1~6l2pou1iqea4mnhenhkm787o56;"
HTTP/1.1 200 OK
Date: Tue, 24 Sep 2013 13:36:45 GMT
Server: Apache/2.2.22 (Ubuntu)
X-Powered-By: PHP/5.3.10-1ubuntu3.8
Expires: Thu, 19 Nov 1981 08:52:00 GMT
Cache-Control: no-store, no-cache, must-revalidate, post-check=0, pre-check=0
Pragma: no-cache
Vary: Accept-Encoding
Content-Length: 163
Content-Type: text/plain
Your number of visits: 1
Server IP: 10.0.0.1
Client IP: 10.0.0.100
X-Forwarded-for: 117.213.X.X
Array
(
[PHPSESSID] => 6l2pou1iqea4mnhenhkm787o56
)
> curl -i http://1.1.1.1/session.php --cookie "PHPSESSID=S1~6l2pou1iqea4mnhenhkm787o56;"
HTTP/1.1 200 OK
Date: Tue, 24 Sep 2013 13:36:54 GMT
Server: Apache/2.2.22 (Ubuntu)
X-Powered-By: PHP/5.3.10-1ubuntu3.8
Expires: Thu, 19 Nov 1981 08:52:00 GMT
Cache-Control: no-store, no-cache, must-revalidate, post-check=0, pre-check=0
Pragma: no-cache
Vary: Accept-Encoding
Content-Length: 163
Content-Type: text/plain
Your number of visits: 2
Server IP: 10.0.0.1
Client IP: 10.0.0.100
X-Forwarded-for: 117.213.X.X
Array
(
[PHPSESSID] => 6l2pou1iqea4mnhenhkm787o56
)
Configure Logging for HAProxy
When we began configuring HAProxy, we added a line:log 127.0.0.1 local0 notice
which sends syslog messages to the localhost IP address. But by
default, rsyslog on Ubuntu doesn't listen on any address. So we have to
make it do so.Edit the config file of rsyslog.
nano /etc/rsyslog.conf
$ModLoad imudp
$UDPServerAddress 127.0.0.1
$UDPServerRun 514
/var/log/syslog so we have to separate them.Create a rule for HAProxy logs.
nano /etc/rsyslog.d/haproxy.conf
if ($programname == 'haproxy') then -/var/log/haproxy.log
service rsyslog restart
/var/log/haproxy.log.Keepalives in HAProxy
Under thelisten directive, we used option httpclose which adds a Connection: close header. This tells the client (web browser) to close a connection after a response is received.If you want to enable keep-alives on HAProxy, replace the
option httpclose line with:option http-server-close
timeout http-keep-alive 3000
Testing Keepalives
Keepalives can be tested usingcurl by sending multiple requests at the same time. Unnecessary output will be omitted in the following example:> curl -v http://1.1.1.1/index.html http://1.1.1.1/index.html
* About to connect() to 1.1.1.1 port 80 (#0)
* Trying 1.1.1.1... connected
> GET /index.html HTTP/1.1
> User-Agent: curl/7.23.1 (x86_64-pc-win32) libcurl/7.23.1 OpenSSL/0.9.8r zlib/1.2.5
> Host: 1.1.1.1
> Accept: */*
>
......[Output omitted].........
* Connection #0 to host 1.1.1.1 left intact
* Re-using existing connection! (#0) with host 1.1.1.1
* Connected to 1.1.1.1 (1.1.1.1) port 80 (#0)
> GET /index.html HTTP/1.1
> User-Agent: curl/7.23.1 (x86_64-pc-win32) libcurl/7.23.1 OpenSSL/0.9.8r zlib/1.2.5
> Host: 1.1.1.1
> Accept: */*
>
.......[Output Omitted].........
* Connection #0 to host 1.1.1.1 left intact
* Closing connection #0
Re-using existing connection! (#0) with host 1.1.1.1, which indicates that curl used the same connection to make subsequent requests.Source: https://www.digitalocean.com/community/tutorials/how-to-use-haproxy-to-set-up-http-load-balancing-on-an-ubuntu-vps
Thứ Ba, 14 tháng 7, 2015
Cyclomatic complexity
Cyclomatic complexity is a software metric
(measurement), used to indicate the complexity of a program. It is a
quantitative measure of the number of linearly independent paths through
a program's source code. It was developed by Thomas J. McCabe, Sr. in 1976.
Cyclomatic complexity is computed using the control flow graph of the program: the nodes of the graph correspond to indivisible groups of commands of a program, and a directed edge connects two nodes if the second command might be executed immediately after the first command. Cyclomatic complexity may also be applied to individual functions, modules, methods or classes within a program.
One testing strategy, called basis path testing by McCabe who first proposed it, is to test each linearly independent path through the program; in this case, the number of test cases will equal the cyclomatic complexity of the program.[1]
The cyclomatic complexity of a section of source code is the number of linearly independent paths within it. For instance, if the source code contained no control flow statements
(conditionals or decision points), such as IF statements, the
complexity would be 1, since there is only a single path through the
code. If the code had one single-condition IF statement, there would be
two paths through the code: one where the IF statement evaluates to TRUE
and another one where it evaluates to FALSE, so complexity will be 2
for single IF statement with single condition. Two nested
single-condition IFs, or one IF with two conditions, would produce a
complexity of 4, 2 for each branch within the outer conditional.
Mathematically, the cyclomatic complexity of a structured program[a] is defined with reference to the control flow graph of the program, a directed graph containing the basic blocks of the program, with an edge between two basic blocks if control may pass from the first to the second. The complexity M is then defined as[2]
An alternative formulation is to use a graph in which each exit point
is connected back to the entry point. In this case, the graph is strongly connected, and the cyclomatic complexity of the program is equal to the cyclomatic number of its graph (also known as the first Betti number), which is defined as[2]
For a single program (or subroutine or method), P is always equal to 1. So a simpler formula for a single subroutine is
McCabe showed that the cyclomatic complexity of any structured program with only one entrance point and one exit point is equal to the number of decision points (i.e., "if" statements or conditional loops) contained in that program plus one. However, this is true only for decision points counted at the lowest, machine-level instructions. Decisions involving compound predicates like those found in high-level languages like
Cyclomatic complexity may be extended to a program with multiple exit points; in this case it is equal to:
The set of all even subgraphs of a graph is closed under symmetric difference, and may thus be viewed as a vector space over GF(2); this vector space is called the cycle space of the graph. The cyclomatic number of the graph is defined as the dimension of this space. Since GF(2) has two elements and the cycle space is necessarily finite, the cyclomatic number is also equal to the 2-logarithm of the number of elements in the cycle space.
A basis for the cycle space is easily constructed by first fixing a maximal spanning forest of the graph, and then considering the cycles formed by one edge not in the forest and the path in the forest connecting the endpoints of that edge; these cycles constitute a basis for the cycle space. Hence, the cyclomatic number also equals the number of edges not in a maximal spanning forest of a graph. Since the number of edges in a maximal spanning forest of a graph is equal to the number of vertices minus the number of components, the formula above for the cyclomatic number follows.[6]
above for the cyclomatic number follows.[6]
For the more topologically inclined, cyclomatic complexity can alternatively be defined as a relative Betti number, the size of a relative homology group:
Alternatively, one can compute this via absolute Betti number (absolute homology – not relative) by identifying (gluing together) all the terminal nodes on a given component (or equivalently, draw paths connecting the exits to the entrance), in which case (calling the new, augmented graph , which is [clarification needed]), one obtains:
, which is [clarification needed]), one obtains:
 , then the fundamental group of
, then the fundamental group of  will be
will be  . The value of
. The value of  is the cyclomatic complexity. The fundamental group counts how many
loops there are through the graph, up to homotopy, and hence aligns with
what we would intuitively expect.
is the cyclomatic complexity. The fundamental group counts how many
loops there are through the graph, up to homotopy, and hence aligns with
what we would intuitively expect.
This corresponds to the characterization of cyclomatic complexity as "number of loops plus number of components".
In order to calculate this measure, the original CFG is iteratively reduced by identifying subgraphs that have a single-entry and a single-exit point, which are then replaced by a single node. This reduction corresponds to what a human would do if she extracted a subroutine from the larger piece of code. (Nowadays such a process would fall under the umbrella term of refactoring.) McCabe's reduction method was later called condensation in some textbooks, because it was seen as a generalization of the condensation to components used in graph theory.[8] If a program is structured, then McCabe's reduction/condensation process reduces it to a single CFG node. In contrast, if the program is not structured, the iterative process will identify the irreducible part. The essential complexity measure defined by McCabe is simply the cyclomatic complexity of this irreducible graph, so it will be precisely 1 for all structured programs, but greater than one for non-structured programs.[7]:80
It is useful because of two properties of the cyclomatic complexity, M, for a specific module:
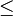 cyclomatic complexity
cyclomatic complexity 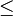 number of paths.
number of paths.
For example, consider a program that consists of two sequential if-then-else statements.
In this example, two test cases are sufficient to achieve a complete
branch coverage, while four are necessary for complete path coverage.
The cyclomatic complexity of the program is 3 (as the strongly connected
graph for the program contains 9 edges, 7 nodes and 1 connected
component) (9-7+1).
In general, in order to fully test a module all execution paths through the module should be exercised. This implies a module with a high complexity number requires more testing effort than a module with a lower value since the higher complexity number indicates more pathways through the code. This also implies that a module with higher complexity is more difficult for a programmer to understand since the programmer must understand the different pathways and the results of those pathways.
Unfortunately, it is not always practical to test all possible paths through a program. Considering the example above, each time an additional if-then-else statement is added, the number of possible paths doubles. As the program grew in this fashion, it would quickly reach the point where testing all of the paths was impractical.
One common testing strategy, espoused for example by the NIST Structured Testing methodology, is to use the cyclomatic complexity of a module to determine the number of white-box tests that are required to obtain sufficient coverage of the module. In almost all cases, according to such a methodology, a module should have at least as many tests as its cyclomatic complexity; in most cases, this number of tests is adequate to exercise all the relevant paths of the function.[7]
As an example of a function that requires more than simply branch coverage to test accurately, consider again the above function, but assume that to avoid a bug occurring, any code that calls either f1() or f3() must also call the other.[b] Assuming that the results of c1() and c2() are independent, that means that the function as presented above contains a bug. Branch coverage would allow us to test the method with just two tests, and one possible set of tests would be to test the following cases:
Studies that controlled for program size (i.e., comparing modules that have different complexities but similar size, typically measured in lines of code) are generally less conclusive, with many finding no significant correlation, while others do find correlation. Some researchers who have studied the area question the validity of the methods used by the studies finding no correlation.[12]
Les Hatton claimed (Keynote at TAIC-PART 2008, Windsor, UK, Sept 2008) that McCabe's Cyclomatic Complexity number has the same predictive ability as lines of code.[13]
Source: https://en.wikipedia.org/wiki/Cyclomatic_complexity
Cyclomatic complexity is computed using the control flow graph of the program: the nodes of the graph correspond to indivisible groups of commands of a program, and a directed edge connects two nodes if the second command might be executed immediately after the first command. Cyclomatic complexity may also be applied to individual functions, modules, methods or classes within a program.
One testing strategy, called basis path testing by McCabe who first proposed it, is to test each linearly independent path through the program; in this case, the number of test cases will equal the cyclomatic complexity of the program.[1]
Definition
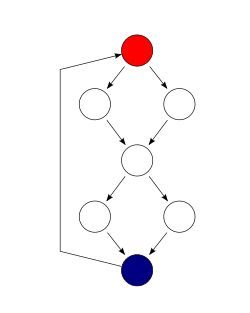
A control flow graph of a simple program. The program begins executing
at the red node, then enters a loop (group of three nodes immediately
below the red node). On exiting the loop, there is a conditional
statement (group below the loop), and finally the program exits at the
blue node. This graph has 9 edges, 8 nodes, and 1 connected component, so the cyclomatic complexity of the program is 9 - 8 + 1 = 2.
Mathematically, the cyclomatic complexity of a structured program[a] is defined with reference to the control flow graph of the program, a directed graph containing the basic blocks of the program, with an edge between two basic blocks if control may pass from the first to the second. The complexity M is then defined as[2]
- M = E − N + 2P,
- E = the number of edges of the graph.
- N = the number of nodes of the graph.
- P = the number of connected components.
The same function as above, shown as a strongly connected control flow graph, for calculation via the alternative method. This graph has 10 edges, 8 nodes, and 1 connected component, so the cyclomatic complexity of the program is 10 - 8 + 1 = 3.
- M = E − N + P.
For a single program (or subroutine or method), P is always equal to 1. So a simpler formula for a single subroutine is
- M = E − N + 2.[3]
McCabe showed that the cyclomatic complexity of any structured program with only one entrance point and one exit point is equal to the number of decision points (i.e., "if" statements or conditional loops) contained in that program plus one. However, this is true only for decision points counted at the lowest, machine-level instructions. Decisions involving compound predicates like those found in high-level languages like
IF cond1 AND cond2 THEN ... should be
counted in terms of predicate variables involved, i.e. in this examples
one should count two decision points, because at machine level it is
equivalent to IF cond1 THEN IF cond2 THEN ....[2][4]Cyclomatic complexity may be extended to a program with multiple exit points; in this case it is equal to:
- π − s + 2,
Explanation in terms of algebraic topology
An even subgraph of a graph (also known as an Eulerian subgraph) is one where every vertex is incident with an even number of edges; such subgraphs are unions of cycles and isolated vertices. In the following, even subgraphs will be identified with their edge sets, which is equivalent to only considering those even subgraphs which contain all vertices of the full graph.The set of all even subgraphs of a graph is closed under symmetric difference, and may thus be viewed as a vector space over GF(2); this vector space is called the cycle space of the graph. The cyclomatic number of the graph is defined as the dimension of this space. Since GF(2) has two elements and the cycle space is necessarily finite, the cyclomatic number is also equal to the 2-logarithm of the number of elements in the cycle space.
A basis for the cycle space is easily constructed by first fixing a maximal spanning forest of the graph, and then considering the cycles formed by one edge not in the forest and the path in the forest connecting the endpoints of that edge; these cycles constitute a basis for the cycle space. Hence, the cyclomatic number also equals the number of edges not in a maximal spanning forest of a graph. Since the number of edges in a maximal spanning forest of a graph is equal to the number of vertices minus the number of components, the formula
 above for the cyclomatic number follows.[6]
above for the cyclomatic number follows.[6]For the more topologically inclined, cyclomatic complexity can alternatively be defined as a relative Betti number, the size of a relative homology group:
- "linearly independent" corresponds to homology, and means one does not double-count backtracking;
- "paths" corresponds to first homology: a path is a 1-dimensional object;
- "relative" means the path must begin and end at an entry or exit point.
Alternatively, one can compute this via absolute Betti number (absolute homology – not relative) by identifying (gluing together) all the terminal nodes on a given component (or equivalently, draw paths connecting the exits to the entrance), in which case (calling the new, augmented graph
 , which is [clarification needed]), one obtains:
, which is [clarification needed]), one obtains: , then the fundamental group of
, then the fundamental group of  will be
will be  . The value of
. The value of  is the cyclomatic complexity. The fundamental group counts how many
loops there are through the graph, up to homotopy, and hence aligns with
what we would intuitively expect.
is the cyclomatic complexity. The fundamental group counts how many
loops there are through the graph, up to homotopy, and hence aligns with
what we would intuitively expect.This corresponds to the characterization of cyclomatic complexity as "number of loops plus number of components".
Applications
Limiting complexity during development
One of McCabe's original applications was to limit the complexity of routines during program development; he recommended that programmers should count the complexity of the modules they are developing, and split them into smaller modules whenever the cyclomatic complexity of the module exceeded 10.[2] This practice was adopted by the NIST Structured Testing methodology, with an observation that since McCabe's original publication, the figure of 10 had received substantial corroborating evidence, but that in some circumstances it may be appropriate to relax the restriction and permit modules with a complexity as high as 15. As the methodology acknowledged that there were occasional reasons for going beyond the agreed-upon limit, it phrased its recommendation as: "For each module, either limit cyclomatic complexity to [the agreed-upon limit] or provide a written explanation of why the limit was exceeded."[7]Measuring the "structuredness" of a program
Section VI of McCabe's 1976 paper is concerned with determining what the control flow graphs (CFGs) of non-structured programs look like in terms of their subgraphs, which McCabe identifies. (For details on that part see structured program theorem.) McCabe concludes that section by proposing a numerical measure of how close to the structured programming ideal a given program is, i.e. its "structuredness" using McCabe's neologism. McCabe called the measure he devised for this purpose essential complexity.[2]In order to calculate this measure, the original CFG is iteratively reduced by identifying subgraphs that have a single-entry and a single-exit point, which are then replaced by a single node. This reduction corresponds to what a human would do if she extracted a subroutine from the larger piece of code. (Nowadays such a process would fall under the umbrella term of refactoring.) McCabe's reduction method was later called condensation in some textbooks, because it was seen as a generalization of the condensation to components used in graph theory.[8] If a program is structured, then McCabe's reduction/condensation process reduces it to a single CFG node. In contrast, if the program is not structured, the iterative process will identify the irreducible part. The essential complexity measure defined by McCabe is simply the cyclomatic complexity of this irreducible graph, so it will be precisely 1 for all structured programs, but greater than one for non-structured programs.[7]:80
Implications for software testing
Another application of cyclomatic complexity is in determining the number of test cases that are necessary to achieve thorough test coverage of a particular module.It is useful because of two properties of the cyclomatic complexity, M, for a specific module:
- M is an upper bound for the number of test cases that are necessary to achieve a complete branch coverage.
- M is a lower bound for the number of paths through the control flow graph (CFG). Assuming each test case takes one path, the number of cases needed to achieve path coverage is equal to the number of paths that can actually be taken. But some paths may be impossible, so although the number of paths through the CFG is clearly an upper bound on the number of test cases needed for path coverage, this latter number (of possible paths) is sometimes less than M.
 cyclomatic complexity
cyclomatic complexity 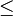 number of paths.
number of paths.For example, consider a program that consists of two sequential if-then-else statements.
if( c1() )
f1();
else
f2();
if( c2() )
f3();
else
f4();
The control flow graph of the source code above; the red circle is the
entry point of the function, and the blue circle is the exit point. The
exit has been connected to the entry to make the graph strongly
connected.
In general, in order to fully test a module all execution paths through the module should be exercised. This implies a module with a high complexity number requires more testing effort than a module with a lower value since the higher complexity number indicates more pathways through the code. This also implies that a module with higher complexity is more difficult for a programmer to understand since the programmer must understand the different pathways and the results of those pathways.
Unfortunately, it is not always practical to test all possible paths through a program. Considering the example above, each time an additional if-then-else statement is added, the number of possible paths doubles. As the program grew in this fashion, it would quickly reach the point where testing all of the paths was impractical.
One common testing strategy, espoused for example by the NIST Structured Testing methodology, is to use the cyclomatic complexity of a module to determine the number of white-box tests that are required to obtain sufficient coverage of the module. In almost all cases, according to such a methodology, a module should have at least as many tests as its cyclomatic complexity; in most cases, this number of tests is adequate to exercise all the relevant paths of the function.[7]
As an example of a function that requires more than simply branch coverage to test accurately, consider again the above function, but assume that to avoid a bug occurring, any code that calls either f1() or f3() must also call the other.[b] Assuming that the results of c1() and c2() are independent, that means that the function as presented above contains a bug. Branch coverage would allow us to test the method with just two tests, and one possible set of tests would be to test the following cases:
- c1() returns true and c2() returns true
- c1() returns false and c2() returns false
- c1() returns true and c2() returns false
- c1() returns false and c2() returns true
Cohesion
One would also expect that a module with higher complexity would tend to have lower cohesion (less than functional cohesion) than a module with lower complexity. The possible correlation between higher complexity measure with a lower level of cohesion is predicated on a module with more decision points generally implementing more than a single well defined function. A 2005 study showed stronger correlations between complexity metrics and an expert assessment of cohesion in the classes studied than the correlation between the expert's assessment and metrics designed to calculate cohesion.[9]Correlation to number of defects
A number of studies have investigated cyclomatic complexity's correlation to the number of defects contained in a function or method.[10] Some[citation needed] studies find a positive correlation between cyclomatic complexity and defects: functions and methods that have the highest complexity tend to also contain the most defects, however the correlation between cyclomatic complexity and program size has been demonstrated many times and since program size is not a controllable feature of commercial software, the usefulness of McCabes's number has been called to question. The essence of this observation is that larger programs (more complex programs as defined by McCabe's metric) tend to have more defects. Although this relation is probably true, it isn't commercially useful[11] . As a result the metric has not been accepted by commercial software development organizations.[10]Studies that controlled for program size (i.e., comparing modules that have different complexities but similar size, typically measured in lines of code) are generally less conclusive, with many finding no significant correlation, while others do find correlation. Some researchers who have studied the area question the validity of the methods used by the studies finding no correlation.[12]
Les Hatton claimed (Keynote at TAIC-PART 2008, Windsor, UK, Sept 2008) that McCabe's Cyclomatic Complexity number has the same predictive ability as lines of code.[13]
Source: https://en.wikipedia.org/wiki/Cyclomatic_complexity
Đăng ký:
Nhận xét (Atom)